How To Animate Objects Rotate In Processing
3D Transformations in Processing

This tutorial explores how translation, rotation and scale — taken together under the umbrella term affine transformations — work in Processing (Java manner). An alternative to matrices, based on a quaternion, is so created to evidence how we can ease between 'keyframes.' To proceed this tutorial from being any longer than information technology already is, the code gists to follow contain just highlights nether word. Full lawmaking for the classes and functions can exist establish here.
This tutorial was written with Processing version 3.three.7 in the Processing IDE (as opposed to Eclipse, etc.). Since coding with multiple objects requires a learning curve, one helpful feature to turn on is lawmaking-completion, to be establish in the File > Preferences menu.
Pushing Matrices with Native Functions
Gild of Operations
Only every bit mathematical operations have a conventional gild (PEMDAS), so do transformations of a shape: translation, rotation, scale (TRS). Until we adjust to this ordering, as Rodger Luo points out in "One Small-scale Trick nigh Transformation in Processing," our code may produce unexpected results.

The magenta square orbits around the top-left corner of the sketch, appearing only 25% of the time, while the green foursquare rotates in identify at the center. To empathise why, we try out six possible orders (TRS, RTS, RST, SRT, SRT, TSR, STR) on the underlying matrix (PMatrix3D for the 3D renderer), then look at the print-out.
Before we look at the results, a sidebar:
Sidebar: Keep Rotations Elementary

The examination above is a simplification of even the simplest use-case where Euler angles are supplied to rotateX, rotateY and rotateZ. Taking that into consideration would mean another six operation orders (XYZ, XZY, YXZ, YZX, ZXY, ZYX) per each of the six above. Instead, nosotros rotate by an bending around an centrality.
The departure between axis-bending and Euler bending rotation is virtually noticeable with the wobbling magenta cube on the far right. A caveat: the centrality should describe merely direction, not scale. This means the vector should have a length of one, and therefore prevarication on the unit sphere. For this reason, it is normalized.
Note
To return to the first lawmaking snippet, by comparison the results of TRS and TSR
with the other iv orders, we can estimate that translate is influenced by rotate and scale, and and so should come beginning. Before we look at translate's definition, nosotros reintroduce the matrix notation used from a previous tutorial on rotation, where each cell corresponds to a float in PMatrix3D:
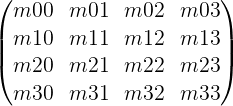
This was supplemented with a more intuitive notation, where the columns correspond the correct (i), upward (j) and forward (k) basis vectors for a spatial coordinate, colour-coded in red 0xffff0000 for i; green 0xff00ff00 for j; and bluish 0xff0000ff for m. t represents the translation. The rows represent the vector components x, y and z. The row value belongs to the column value.
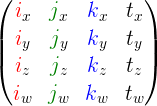
Were nosotros to represent a matrix with a 2D array instead of as an object,
programming conventions would propose that columns belong to the rows. This could then be re-envisioned as
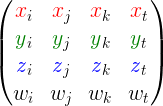
This point is belabored because (1.) to understand transformations we must switch between these 2 orderings; (2.) transposing a row index with a cavalcade alphabetize is an easy mistake to brand; (three.) PMatrix3D's loose bladdersouth, make it easy to switch between thinking in rows and in columns.
Translation and Scale
With that nether our chugalug, permit's wait at the definition for translate in the source code
Calibration, by comparing, is straightforward:
Taken all-together with rotation, these operations can be represented as
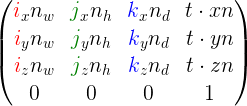
Width (west), height (h) and depth (d) are the components of non-uniform scalar n. For n, multiplication is defined as five * due north = (v.x * n.due west, 5.y * n.h, v.z * north.d).
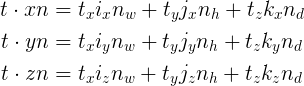
What this does not adequately capture from the source code is the += in translation and *= in scale. These operations are cumulative; they do not set the matrix to a item translation or calibration. This aggregating comes into play when we nest 1 transformation within i another.
Nesting Transformations
To illustrate nested transforms and spatial locality, consider a model of the solar organisation prior to the appearance of Newtonian physics. The sun is at the origin of the solar system; the world is a child of the sun; the moon, a child of the earth. Humanity'due south place within this universe could be solipsistic, geocentric or heliocentric. With Processing's built-in tools, such a model tin be coded as

With each pushMatrix, a matrix is pushed onto a stack data structure. Stacks follow Terminal-In, Start-Out ordering (LIFO), so nosotros create and utilize transformations in the guild 1–two–3; nosotros remove (popMatrix) them in the order 3–2–1. Should we wish to replicate this process independently, we could take an approach such every bit
Where applying the matrix inverse reverses the impact of its multiplication, and could be idea of as matrix division. Care should exist taken, nonetheless, matrix multiplication is not commutative, i.due east., m * n != n * chiliad.
Processing calls multiplication of this matrix m by an operand to the correct, n, apply. The multiplication of this matrix n by an operand to the left, m, preApply.
Trees / Hierarchies
Conceptually, this 'solar organisation' can be thought of as a tree. Each node tin can take multiple children, merely simply 1 parent. E.thou., the dominicus has eight planets; Jupiter, 69 or more moons. If a node has no parent, it is the root node; if it has no children, it is a leaf node. This leads to a hierarchical structure, where whatsoever change to the root node cascades down to its children, grandchildren and all ancestors thereon. The distance of a node from the root is its depth; a maximum depth for the tree tin exist found by seeking the deepest leafage node.
This hierarchy may expand in either direction, moving up to the Milky Way Milky way, or down to the limbs of the human body. We visualize information technology with tabular indents, as in Unity's hierarchy panel, or with nodes and edges.
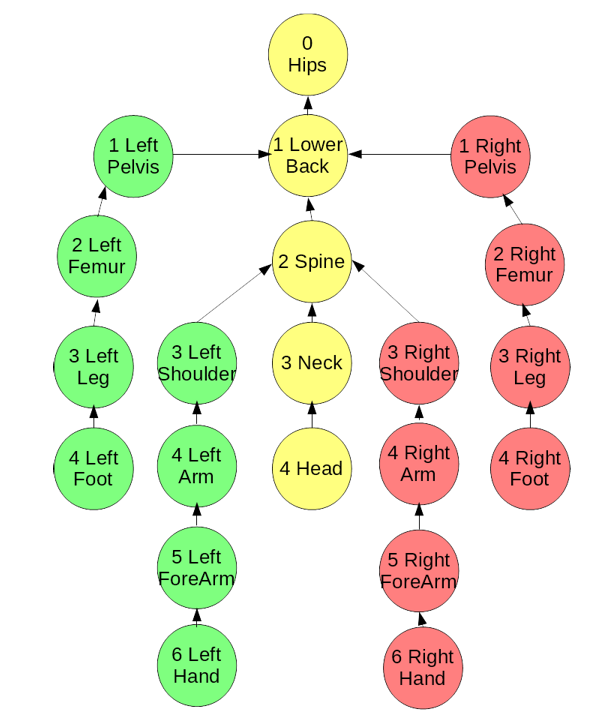
Since a goal of this tutorial is to open new possibilities for animation, we note that anthropoid skeletal rigs can exist described by such a tree.
Decomposing Transformations
Processing functions model and screen let us cache coordinates relative to a tree node; however, if nosotros want to know the translation, rotation and calibration of a matrix, nosotros decompose information technology. To exercise and then, we refer to this give-and-take at Stack Overflow and 3.js, keeping in mind that Processing flips the vertical axis from the OpenGL standard. For the P2D renderer, we use
The manner getMatrix and these decompose functions work may exist unfamiliar. We await a role like getObject() to return a new instance of that data-type. Creating a new object every frame of blitheness is expensive, so functions that work with expensive objects have an 'out' parameter. This 'out' is an example of that object that has already been created; the object'southward values are set within the function. Additionally, if 'out' is non supplied, getMatrix(); doesn't know whether nosotros want a 2D or 3D matrix, and we have to cast the event,(PMatrix3D)getMatrix();.
Although 3D is our focus, annotation that Processing's other 2D rendering modes, JAVA2D and FX2D, rely on the AWT and JavaFX libraries respectively. Readers interested in conveying the concepts beyond will demand to research how those libraries implement a transform matrix.

Back in 3D, the biggest departure is that we have many means to stand for rotation. Here, we apply Euler angles. Finding the determinant is required for extracting a matrix'south calibration; information technology'due south tidy enough in 2nd, but is heftier in 3D.
We have rotation club — XYZ — for granted; to exist robust, we'd accept to account for all possible orders. Nosotros also assume a fixed camera. If it is animated with the camera office, the matrices representing the sketch's projection, project-model-view, and then on may be worth taking into account. Such matrix information tin be accessed by creating a PGraphics3D variable to which (PGraphics3D)g; is assigned later on size is called in setup.
A Custom Transform
Transforms that utilize a quaternion are an alternative to the matrix-based arroyo above. Before creating our own, we'll jot down some criteria we'd similar to come across.
Writing A WishList
We want our transform to be
- Consequent — two functions with the aforementioned proper name behave the aforementioned mode.
- Curtailed — as much lawmaking every bit possible is shifted into
setupand into class methods. The transform is animated in thedrawloop with few lines of code. The transformation of one shape influences just that shape. - Clear — functions are named and so we can distinguish between transformations of a shape by a value, to a value, or between values over a step in time. We can debug transforms visually and in the console.
- Capable — transforms can be parented to one another. The position, rotation and calibration of a transform in world space can be accessed and mutated (without having to decompose a 4x4 matrix). The right, up and frontward axes of a transform tin be accessed.
Fair alert: since we're deviating from Processing'south default tool-set, a lot of setup will be required before we see a payoff.
Transformable Elements
It is common for programming languages to represent a color, coordinate, Euler angles, non-uniform scalar, normal, direction and just about any triplet of real numbers with a vector. An advantage in doing and then is that at that place is less code to write and maintain. Additionally, functions are less picky; we won't throw an error because we've supplied a vector to a function that wants a coordinate. Last, since much joy in creative coding is synaesthetic — representing time as calibration or space as colour, for instance — the borders between senses are easier to cross when one data container is all we need.
A disadvantage arises from its obscurity. When learning vectors, the blackboard explanation bears footling resemblance to how they're used in code. Vector functions are inappropriate to the information stored in x, y and z.
Tutorials and libraries with all-purpose vectors are easy to discover, then for multifariousness's sake we'll separate these triplets out. There is a hazard to to taking this route, indicated by the Circumvolve-ellipse problem, which volition not rear its caput immediately; we give it a proper name now so equally to better spot information technology later. Mattias Petter Johansson has a great discussion most this (targeted at JavaScript) in "Composition over Inheritance."
Insofar as these various data containers are similar, we want to guarantee that they share behaviors: the ability to compare i against the other and therefore to be sorted; to check for approximate equality between floatsouthward; to reset to a default value; to copy another instance of the aforementioned type with a fix function. We create an interface to code this guarantee. This volition too help united states of america maintain consistent office names.
To follow through on this guarantee, we'll need a reliable fashion to approximate floats. For this, nosotros refer to The Floating-Bespeak guide. While we're at it, now's a practiced time to cover other needed utility functions, namely floorMod.
The % operator will return a negative value when the right-hand operand b is negative. floorMod returns a positive value. This is handy for setting an Euler bending to a range 0 .. TWO_PI or screen-wrapping a moving object (as in Asteroids). The naming convention for these two functions varies amidst programming languages; we stick with that of Java's Math library, which includes floorMod for intdue south and longdue south.
Tuple
We start past creating an abstract course equally a parent for signal-like types with three named floats. For those unfamiliar, a form is commonly analogized as a 'pattern' for instantiating object; an abstruse class is not intended for direct instantiation, but for passing on blueprint data to kid- or sub-classes.
In the large movie, this approach will consist of pushing upward into abstraction: if we find ourselves writing the aforementioned role repeatedly for each class that extends Tuple, then we can move that function into Tuple itself.
Because classes defined within a Processing .pde file need to be static to ascertain a method such as static Tuple sub(Tuple a, Tuple b) { /* … */ render new Tuple(x, y, z); }, we adopt an unconventional format: binary methods like addition and subtraction accept two inputs a and b. The event is assigned to the tuple instance that chosen the method. For unary methods, such every bit a vector's normalize method, the input is named in.
When comparing two Tuples for the purpose of sorting them, the compareTo function mandated by the Comparable interface returns -1 when Tuple a is determined to be less than b, and should precede b in a list sorted in ascending order; when a is greater than b, one, and should follow b; when the two are equal, 0. The ternary operator is a shorthand for if(a.z > b.z) { return ane; } else { /* … */ }. This means that z is the most important criterion when sorting two Tuples, followed by y and and so x.
Next up, a spatial coordinate class:
Coordinate
For now, this class does non need much. Why carp? An case of where the distinction between coordinate and direction comes in handy is the lookAt method. When we desire one object to look at another, we can create lookAt(Coord origin, Coord destination, Vector up);. When we want it to look in a direction, we can write lookAt(Coord origin, Vector lookDir, Vector upward);. Furthermore, were we to support a matrix class, we could add a due west field to Coord to support multiplication between them.
Where possible, the principle of chainability is kept through having math operations return Tuple;, return Coord;, and and so on. This can lead to confusion later. Suppose we add together two coordinates, Coord c = new Coord().add(new Coord());. This throws an error because the value returned is of the blazon Tuple. Information technology makes more sense to say that Coord add together(Vector 5); represents moving from ane spatial coordinate to another by a direction. The larger indicate is that sometimes a designer withholds functionality — even when adding it would make life easier — because information technology distorts how lawmaking models reality. The GDC talk "Understanding Homogeneous Coordinates," left, is helpful in explaining the addition of points and directions.
Management
This class is called Direction, not Vector, for a reason. Directions which instruct the estimator how to translate low-cal and shadow on a surface are called normals. These are not necessarily normalized, and not to be confused with the normalize part. Shown the epitome to follow, Processing computes low-cal and shadow on our behalf when the normal part is absent from beginShape, so this step is optional.
A major deviation between vectors and normals is the manner a normal's scale is calculated when the surface it represents change scale. Furthermore, normals cannot be added to a spatial coordinate or created from subtracting two coordinates.
Nosotros prioritize those vector functions upon which future operations depend. More can be implemented by looking at the PVector class; there are also functions, such as reflect and scalar projection (see Shiffman's video to the left), non contained in PVector but dainty to have.
Dimension
The next Transformable is a nonuniform scalar, which has width, acme and depth. Beneath are a few highlights.
The best way to understand this grade is to think through why a vector is a bad way to correspond dimension. First, although minor, are variable names: x, y and z do not draw this class'south fields. Second, while a vector resets to (0, 0, 0), a dimension resets to (1, 1, 1). Third are key differences in how addition, subtraction, multiplication and division piece of work. Adding a single bladder value to a dimension means adding a uniform scalar to a nonuniform scalar; a unmarried float tin't be added to a vector. As we saw before when decomposing a matrix, vectors have scalar, dot and cantankerous production operations; they cannot be multiplied by three separate floats.
Rotation
Since quaternions were introduced in some other tutorial, we'll but touch new methods.
The forward, right and up functions allow united states of america to access and display the orthonormal basis of a shape. These are the unscaled i, j, and k columns of a matrix. Quaternion multiplication provides the analog to nesting one call of pushMatrix inside another. If we recall that a quaternion can be represented either equally iv numbers or every bit an imaginary vector and a existent number,
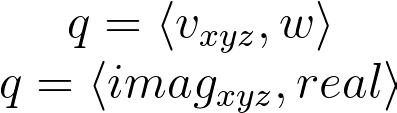
we can express quaternion multiplication equally
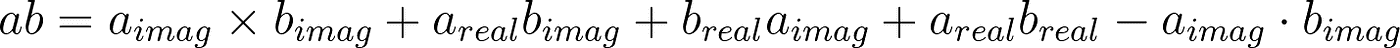
Segmentation, which depends on the capsize office, is a crude analog to popMatrix. Like 2D complex numbers, a quaternion's changed depends on its cohabit,
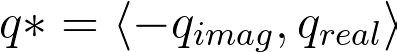
which is the negation of its 10, y, and z components. The cohabit is and then divided by the quaternion'south magnitude-squared.
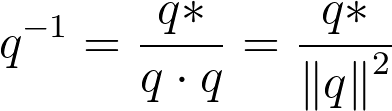
Returning to our wishlist, it'southward not clear that rotateX and visitor are functions to rotate geometry past an bending around the ten-centrality. Furthermore, this could be another case where functionality should remain unimplemented. Rotation by ten, y and z encourages sequential Euler angle rotations, rotation.rotateY(theta).rotateZ(theta);, a habit we want to get away from.
Brittle Class Hierarchies
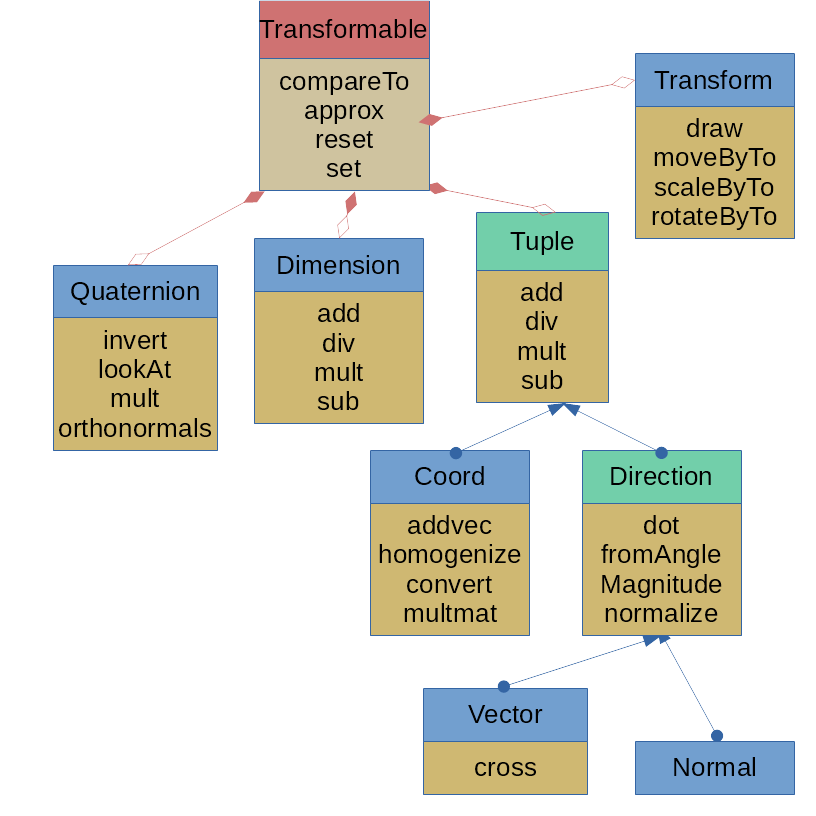
Fans of the meta volition notice that the hierarchical tree we're developing describes the lawmaking's blueprint itself.
In the diagram, left, interfaces are color-coded in red; abstract classes, in green; and classes we instantiate into objects, in blue. Organizing these classes is a negotiation between what an object is, what it does and what kind of data it has. The negotiation is dirty past the fact that any action a class does can be coded as a method or as a 'behavior' object the class has.
Any satisfaction to exist gained in arranging classes neatly is flustered by the brittleness of hierarchies. Such diagrams offering the impression that coding can be and is ever planned in advance. That frequently conflicts with creative coding's emphasis on prototyping, iteration and exploration. Once we add new features, this illusion of order collapses.
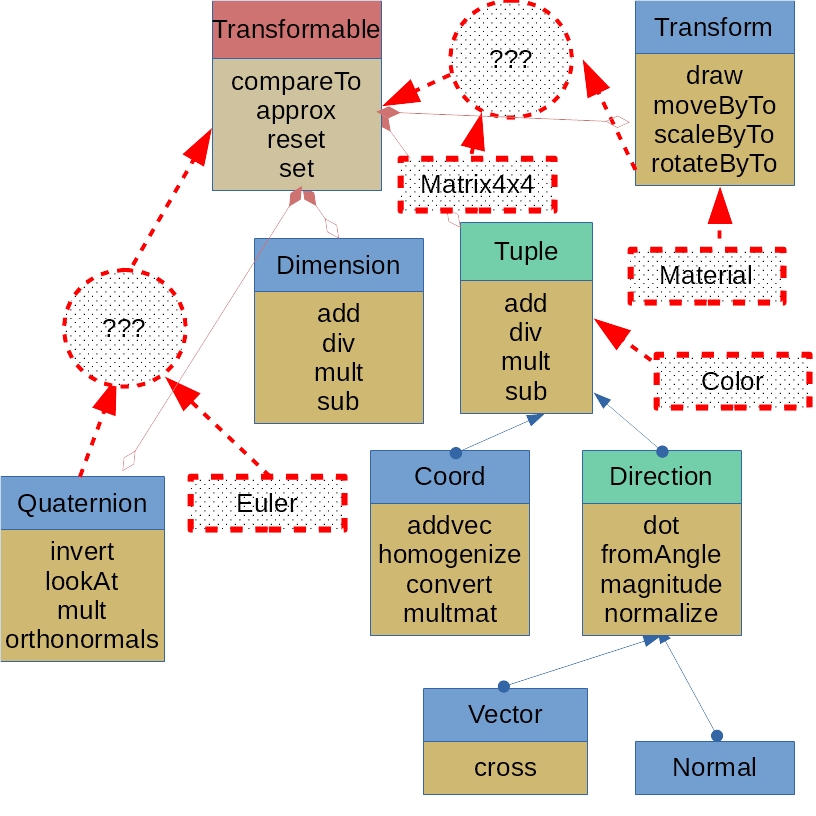
Eventually, an introduced course will find multiple candidates to be its parent; or will for the sake of belonging find the least unlikely parent to extend. A child class volition inherit from its parent a behavior that undermines its identity, but which information technology cannot conceal. A parent will concur onto information information technology doesn't demand for the sake of its children. Two classes which should vest together conceptually will have so few information types in common that all we tin can practice is add together a marker interface for them. The closer to the root these problems occur, the bigger the hassle in revising code.
Having raised the issue of inheritance hierarchies, resolving it in Coffee would have us far afield of the subject field at hand. Nosotros motion on to the transform form, trusting that those interested in resolving the above will find a blueprint pattern best suited to the job.
Transform Classes
We may animate not but a coordinate in sketch space, but likewise a texture coordinate that maps an epitome onto a model'south geometry. For that reason, nosotros split a material from a transform, and make a abstract TransformSource parent class. Convenience is the primary consideration for this class: a bulk of functions are wrappers that provide intuitive function names.
These wrappers allow united states to meet our criteria, specifying when a function transforms by a value and to a value. Since we cannot avoid PMatrix objects entirely, we provide conversions similar to those before, decomposing into quaternions instead of Euler angles.
For the Transform class, nosotros extend the above and add together the following
For diagnostic purposes, we depict red, dark-green and blue lines showing the transform's axes. The parent field allows transforms to nest one within the other, replicating the nested calls to pushMatrix. This complicates our ability to find the position, rotation and scale of the transform relative to the sketch, not its parent.
An culling would be to create a tree or node class which has a Transform object. For that approach, Stack Overflow discussions are here and here.
Applying Transformations
To employ a transformation to a point, we add methods to the Tuple class. Convention sometimes call these applyTo and reverse which object owns them. For example, a quaternion would have the office applyTo(Tuple t).
Equally seen in a higher place, translation is influenced past rotation and scale. And then while rotation has a directly correlation with multiplication by a quaternion, and scaling with multiplication past a dimension, translation is the addition of ii tuples after multiplication by rotation and calibration.
Example: Spirograph

With the higher up in identify, we can try for a digital Spirograph, dressing it up with translucent backgrounds and blend modes.
Adding a translucent groundwork console to a sketch is a common technique amidst creative coders to give animations a contrail or, depending on the blend mode, a diaphanous look. In 2D, fill(0x7f000000); rect(0, 0, width, height); volition suffice; 3D is less intuitive, given the potential of a moving photographic camera.
Because a bespeak could pass backside the background, nosotros disable all activity related to testing depth. If we animate the camera, nosotros first cache its default orientation in a PMatrix3D, then laissez passer that into the role. Later, we'll introduce an alternative that uses rendering techniques better suited to 3D geometry.
A Custom Mesh
In an earlier tutorial on 3D modeling we introduced .obj files, which tin can exist imported into Processing via loadShape. By disconnecting from matrix transformations, we've lost the convenience of this function and the object it returns, a PShape. In the following section, we develop our ain.
WaveFront .obj File Format
To empathize what we've lost and how information technology can be regained, let's review the .obj file format. The example below describes a cube.
Information is preceded by a fundamental: the object's proper noun begins with o; a vertex, with 5; a texture coordinate, with vt; a normal, with vn. Information for the face, preceded past f, are most in demand of explanation. Simulating the cube's front end face volition help to understand.
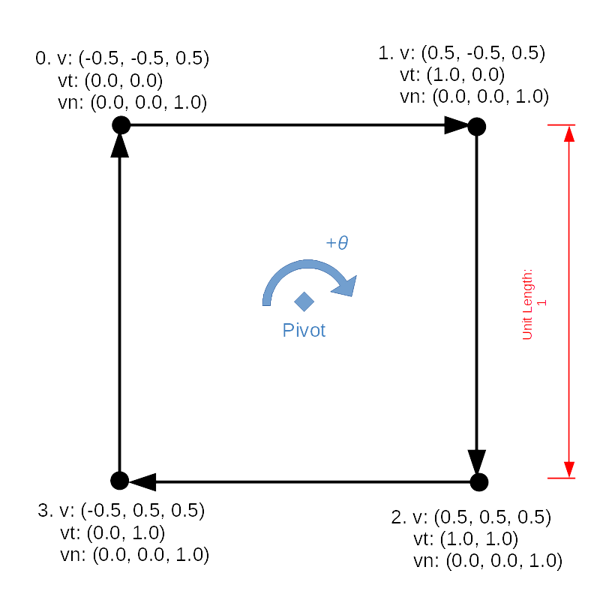
The pin point around which all vertices rotate is (0, 0, 0), then nosotros start winding at the top-left corner, and so continue clockwise to the superlative-right corner. (Instead of using 0.five, nosotros can dub the border A (-i, -1, i), B (1, -1, 1), giving it a length of 2.) Because the forepart face of this cube shares each of its four edges with four other faces, and because each edge shares its vertices with other edges in this face and in other faces, we have to store data without duplication and access it out of sequence.
If we think of the information in the v, vt and vn sections as arrays (assuming that they have been calculated and included) the face section contains indices to these arrays, separated by a forward slash /.
Mesh Class
With this in listen, we tin can parallel the .obj format in working memory with
We need to be explicit about passing by reference versus passing by value, a silent stardom in Coffee. Whenever we laissez passer an object into a role, we are passing a reference to its memory address, not an independent value which can be changed without also changing the original. In society to leave the original object intact, we copy the archaic floats that information technology contains.
We'd like load mesh information from an .obj file one time, and then share this 'template' amid many entities that are transformed independently of one another. Too, we want to manipulate a mesh procedurally then export the changes as an .obj file. An entity'southward transformation would have no effect; we'd demand to copy the mesh information, then dispense the mesh and not the entity. (For those familiar with Blender or modeling software, this is the distinction between Object and Edit mode.)
Acquiring Faces and Vertices
When accessing and mutating that data, for convenience nosotros'll desire not the indices, but the data pointed to past those indices. To do this, we create a vertex and face up grade:
and
To recall them from the mesh, we render to the Mesh class to include
These provide a workaround to limitations of PShape, whose getChild, getVertex, getNormal, getTextureU and getTextureV functions are messy. Moreover, this workaround follows a pattern for augmenting Processing to handle intermediate projects: what we demand is already at work behind the scenes; we expose it while subdividing tasks for a finer granularity.
Even then, the ability to edit a mesh exposed past these classes is fairly basic. Edges, for example, are nowhere represented; the ability to find the neighboring faces of a face is absent. Greater nuance may be found in the one-half-edge data structure, for which a library, HE_Mesh, is available.
Importing An Obj File
Given the linear format of an .obj file, loading and saving 1 is easier to do than nosotros might first imagine. We've simplified Processing'south import function in that we assume a file will e'er include texture coordinates and normals. A robust part would handle scenarios in which the information is absent by, for instance, supplying default values.
At the end of our import function, nosotros await a fixed number of coordinates, faces, etc. Yet, at the beginning, nosotros don't know how many an .obj file will contain. For that reason, we create lists which, unlike arrays, tin can aggrandize when new information needs to be added. We convert these to fixed-size arrays with toArray at the function's end.
This task falls under the heading of tokenization. Processing'due south loadStrings role has already taken care of splitting up the selected file past line-pause into an array of Cords. On each line, information is dissever by whitespace, and then split("\\south+"); separates tokens by that. The first token determines which category nosotros go to in a large if-else cake while the remaining tokens are parsed equally either bladders or, in the example of faces, intsouth. Faces is a special case in that information technology is cleaved into sub-groups by /.
Exporting An Obj File
Writing a file is easier than importing 1. A library to export .obj files, courtesy Nervous System, is also available. The 1 play a trick on that may be new is how to avoid chain of Strings with the + operator. Two tools to aide with that are the Cord.format function and the StringBuilder object.
We exit aside the thing of importing materials, since a material'south capability varies greatly across graphics engines, and depends on underlying shaders.
Material Grade Definition
Instead, materials are created through a Textile class.
As a reminder, emissive color is given off without any lighting in the sketch. Ambient colour responds to atmospheric lighting with no discernible management or source. Specular color defines the glint that reacts to directed light sources. Shininess is the gloss of a material. This abstract super class can and so be extended to handle a texture.
Texture mode dictates how Processing interprets the texture coordinates supplied to vertex. Processing uses the pixel size of the source image by default, non coordinates in the range 0 .. 1. Using NORMAL allows source textures of varying dimension to exist mapped consistently onto a shape. Texture wrap dictates what happens when a texture coordinate exceeds the range set by texture fashion; REPEAT allows a texture to wait like a wallpaper.
Drawing An Entity
Every bit mentioned earlier, nosotros must distinguish between the animation of underlying mesh and of an object in space which draws that data. For this reason, we create an Entity grade.
The v, vt, vn and wr variables ensure that no transformation becomes permanent. For now nosotros, are simplifying our Entity class; a more adult approach would exist to create an Entity-component organization. To see this in activity

nosotros create iii entities, each of which has an blithe material and transform. The magenta figure, bottom-center, retains a copy of the mesh information, which it animates in draw. To see what does and does non carry across upon export, and how the qualities which are non exported can be recreated, we import it into Blender and into Unity.
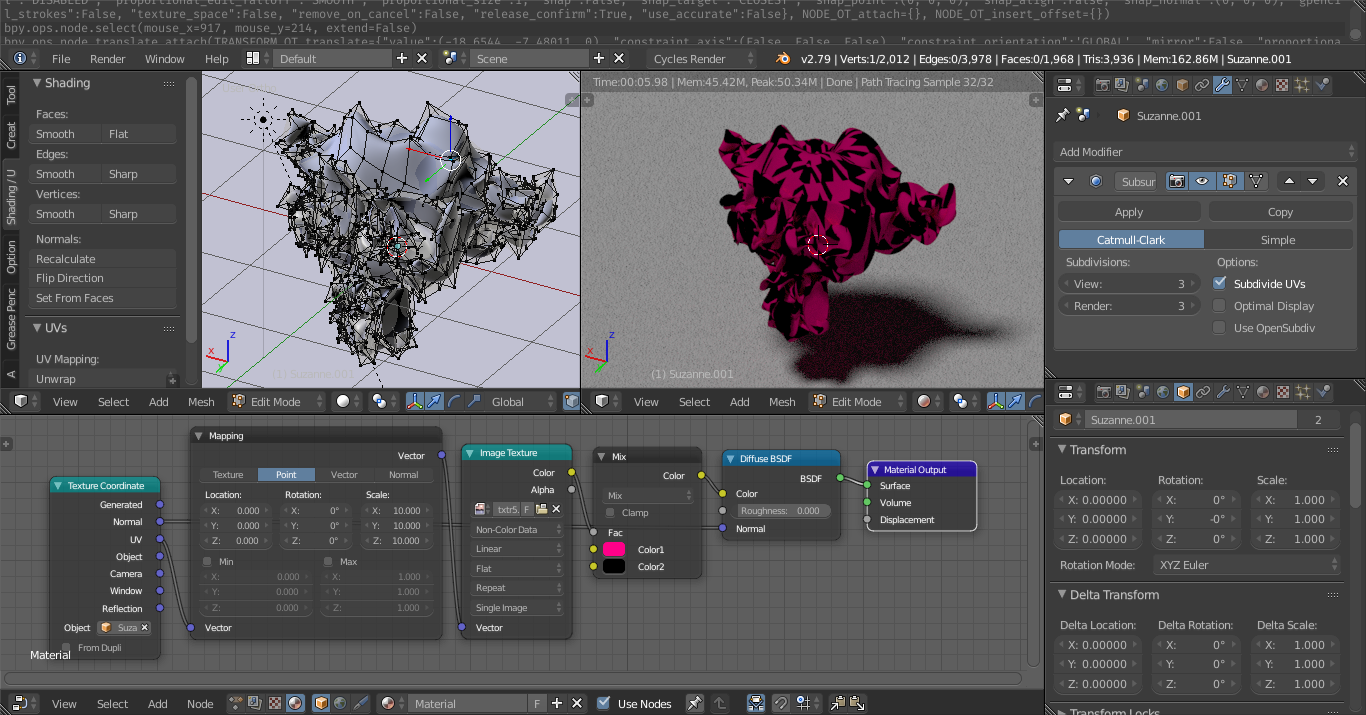
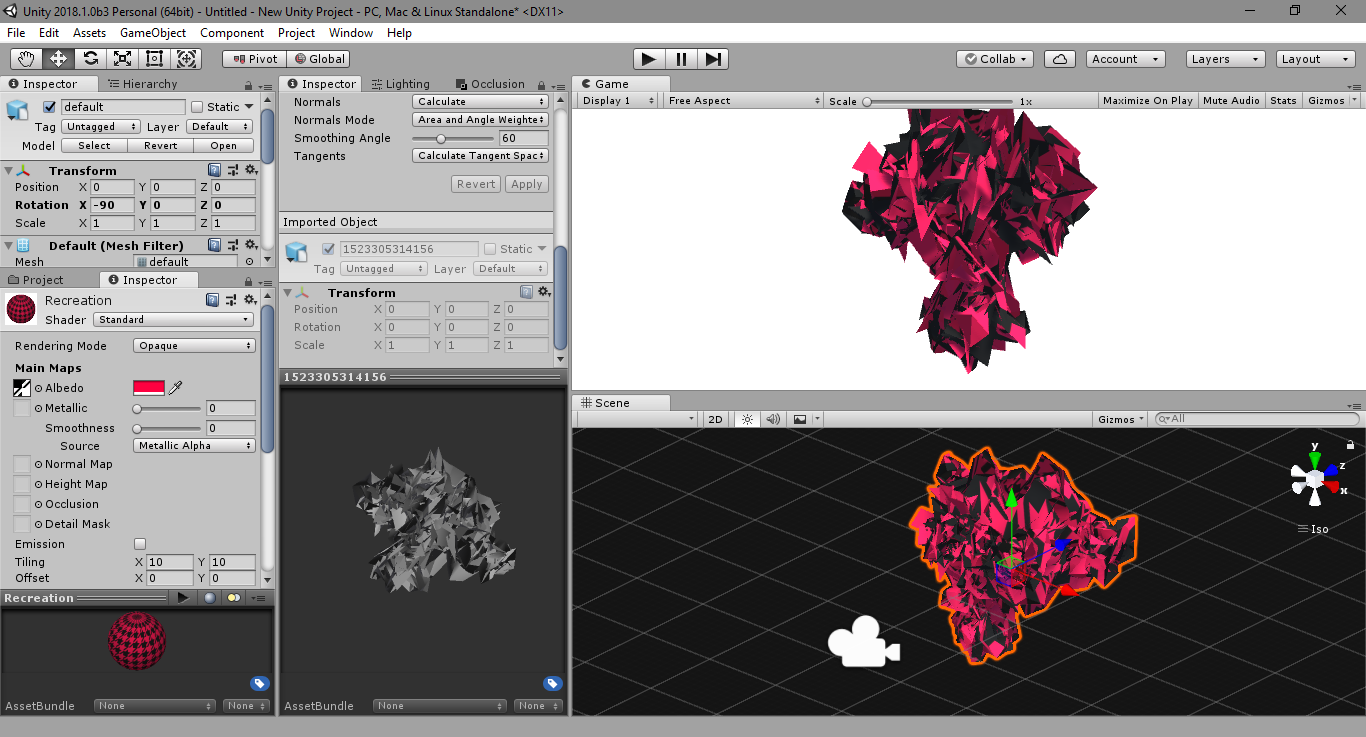
Neither the scaling of the UV coordinates by the material nor the rotation past the transform are retained, merely the addition of random values to the underlying geometry are. Both Unity and Blender provide the option to recalculate the normals according to their own earth coordinates.
Easing
A major reason to use quaternion-based transforms is to ameliorate facilitate easing (or tweening) between positions, rotations and scales. Because we don't know in advance which kind of tweening we'd similar to utilize (lerp, ease-in, ease-out, etc.) we externalize this behavior. First, nosotros lawmaking an umbrella class to embrace all the variety
The passing of behaviors as objects dorsum and along is not every bit natural to Coffee equally information technology is to JavaScript. The library coffee.util.function offers some classes, and nosotros can too specify a @FunctionalInterface with an annotation if nosotros need more. This parent class handles the logic for easing betwixt a start and finish keyframe or for easing between an array. The logic specific to each kind of easing, applyUnclamped, is left to subclasses to ascertain. Equally an case, to ease between tuples, we use
referencing Ana Tudor'due south "Emulating CSS Timing Functions with JavaScript" for ease-in and ease-out. The easing of dimensions and quaternions follow a similar blueprint, and so we won't encompass them here. We tin can then lump these together into a transform easing beliefs.
Were we to brand any provision for a Color course, nosotros could determine upon easing between colors in RGB and HSB, then incorporate that into Material easing classes. For those interested in such a possibility, a previous tutorial on color gradients may provide reference. Put into effect, these look like
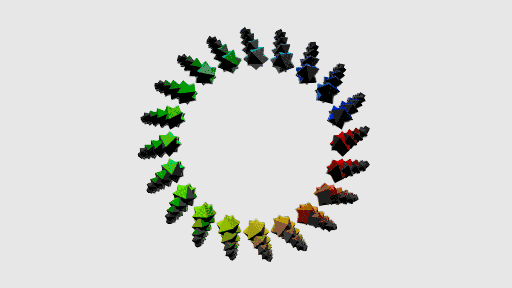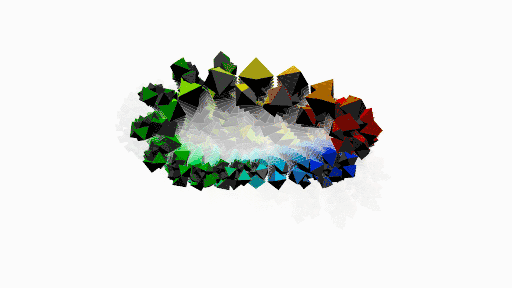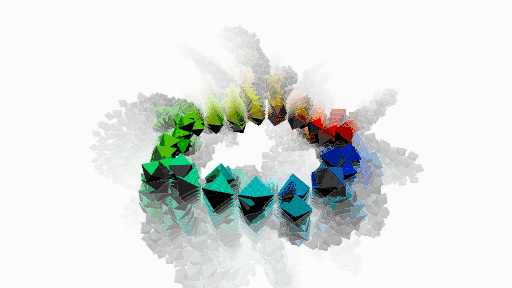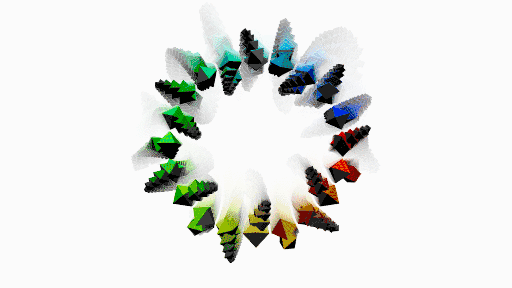
Because frame rate is now a business organisation, we apply a simpler diamond geometry. Instead of creating a rectangle shape with translucent fill, we employ createGraphics to create a second renderer. This tin can accept a transparent background.
In draw, we update the 2nd renderer, then blit it onto the principal sketch renderer with image. This has the benefit of rendering at 1 scale, then either upwardly- or downscaling to the display. We have greater control over how we capture stills depending on which renderer saves the image. A disadvantage is that residue may appear on the edges of geometry when a translucent background is used on the secondary renderer.
Conclusion
When reaching the cease of a start iteration, it is worth returning to our wishlist to see if we've met any of our goals. Additionally, we can ask what artistic potential is opened past the coding we've done. One possibility is to wait at examples of the Twelve Principles of Animation and prepare ourselves the challenge of recreating them. Another would exist to explore basic skeletal and pendular movements enabled by nested transformations.
Source: https://behreajj.medium.com/3d-transformations-in-processing-de11acdd1fbc
Posted by: slayunty1998.blogspot.com

0 Response to "How To Animate Objects Rotate In Processing"
Post a Comment